Python Sortest Path

Jugando a Advent Of Code me topé con el ejercicio número 12. Este ejercicio requería encontrar el camino más corto hasta la cima de una montaña. Para ello se da al jugador un mapa topográfico de 26 niveles de altura indicados por letras del abecedario, una posición inicial y una posición final.

Las restricciones son muy simples:

• Se puede mover hacia arriba, abajo, izquierda y derecha. No en diagonal.
• No se puede mover a casillas que estén a más de una unidad de altura de diferencia de la posición en la que se está.

Yo traté darle un punto de vista diferente al ejercicio y en lugar de buscar la distancia más corta entre dos puntos, trataría de encontrar todos los puntos alcanzables y la distancia más corta hasta cada uno de ellos dada una posición de origen. Estaría claro que mi forma sería más costosa en tiempo de ejecución debido a que calcularía la distancia hasta cada uno de los puntos del plano.

Ya existen multitud de algoritmo que encuentran la ruta óptima entre dos puntos basándose en grafos y en longitudes de Manhattan. Yo quería ponerme de reto no utilizar estos algoritmos y crear un algoritmo por mis propios medios que sea capaz de calcular la distancia a los puntos más cercanos de un golpe.

Además, quise poder añadir zonas prohibidas en el plano. Que pudieran representar, por ejemplo, propiedades privadas en las que no se pudiera acceder. Por lo que las restricciones quedarían:

1. Se puede mover hacia arriba, abajo, izquierda y derecha. No en diagonal.
2. No se puede mover a casillas que estén a más de una unidad de altura de diferencia de la posición en la que se está.
3. Utilizar el razonamiento lógico para realizar un nuevo algoritmo que pudiera encontrar el camino más corto a cada uno de los puntos del plano, dada una posición de origen.
4. Poder añadir zonas prohibidas al mapa topográfico que no puedan ser accesibles.
5. No utilizar librerías externas.

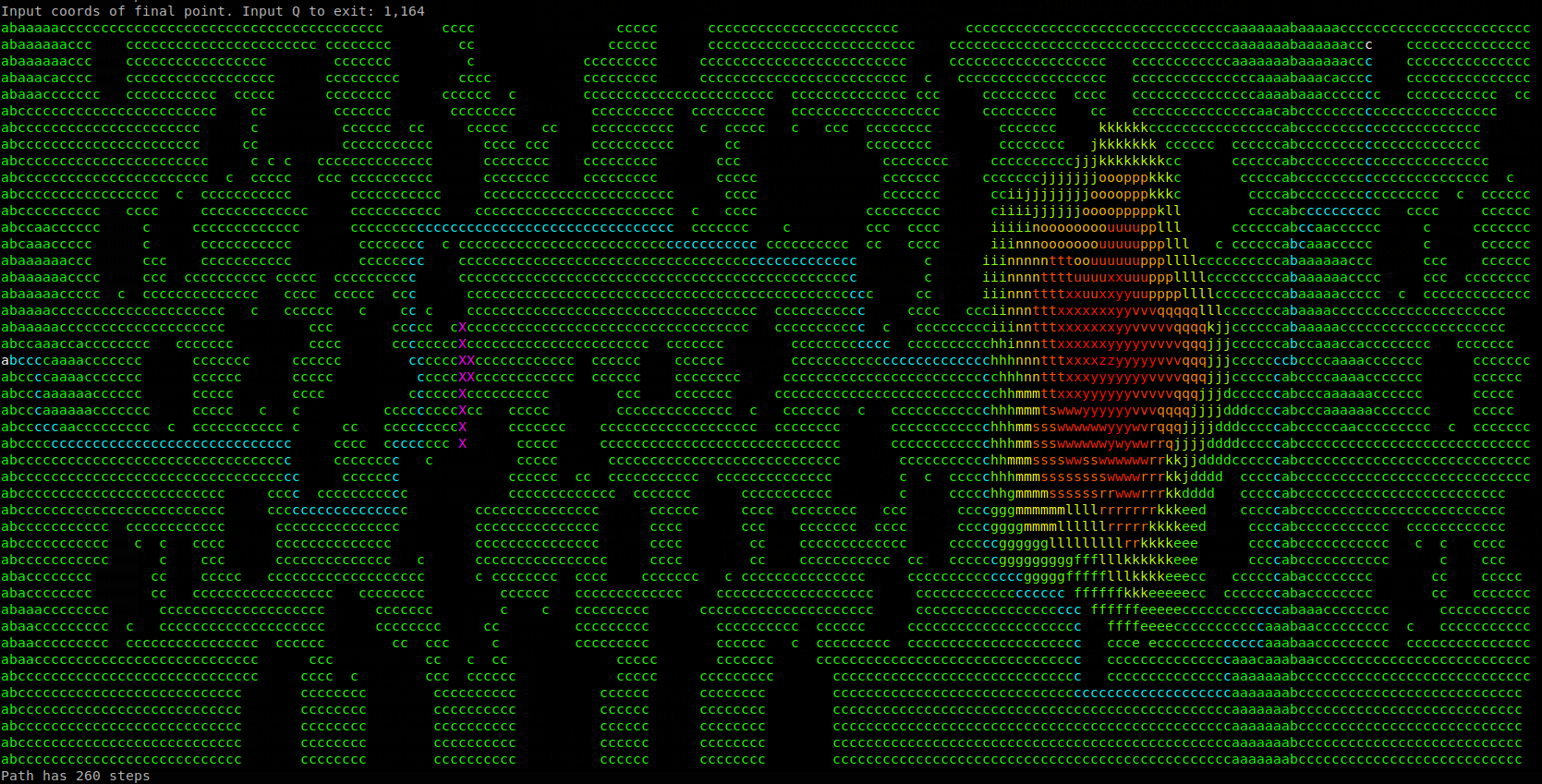
El primer paso, fue poder visibilizar el mapa topográfico en la terminal. Este mapa debería servir para ver de un vistazo los puntos accesibles del plano y su altura correspondiente mediante colores.

El siguiente paso era diseñar el algoritmo. Esta tarea llevó varios días hasta dar con el método correcto que lograra devolver la distancia a todos los puntos. A continuación, explico brevemente su funcionamiento.

• Se crea un poliedro que represente todos los movimientos posibles en un radio de X unidades. Dada la regla uno la figura se correspondería con un octaedro. Si se pudiera mover en diagonal la figura se parecería más a una esfera.
• Se selecciona el punto origen y se crea un plano (bidimensional) con los puntos a una altura alcanzable de acuerdo a la regla 2.
• Se coloca el octaedro sobre del punto inicial en el plano y se disminuye la altura del octaedro para que vaya atravesando el plano. Los puntos que interseccionan el octaedro con el plano corresponderán a la distancia entre esos puntos hasta el punto del plano que está sobre el octaedro. Debe tenerse en cuenta zonas inalcanzables, como barrancos o montañas, y zonas prohibidas por la regla 4.
• Se guarda la distancia a los nuevos puntos sumando la distancia del punto inicial al origen (punto del cual se quieren descubrir todas las rutas más cortas).
• Se repite este proceso para todos los puntos hasta completar el mapa topográfico. (Se cambia el punto inicial por el nuevo punto).
• Conocida la distancia a cada uno de los puntos, puede calcularse el camino más corto de forma sencilla.

En las siguientes imagenes puede visualizarse el proceso de cálculo de las distancias. El color verde indica cercanía y el rojo lejanía. Un cambio brusco de color entre verde y rojo significa que se le ha dado la vuelta al contador de colores, por lo que hasta el cambio de color habrá una distancia de 255 unidades. Finalmente, una casilla en color cian representa sobre qué punto está ubicado el octaedro en esa ejecución.

Tras unos pocos minutos se calcula el mapa de distancias y se podrá introducir las coordenadas de un punto final para que la ruta sea representada en el mapa topográfico.

Es posible que haya varios caminos con la misma longitud hasta el origen, el script está programado para devolver el primer camino que encuentre.

La eficiencia del algoritmo es exponencial O(cⁿ).

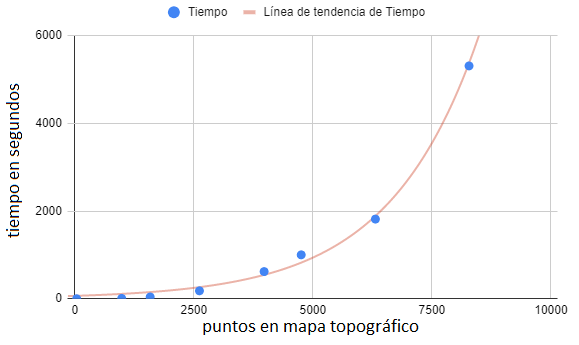
No será el más eficiente, pero es el mío.